Week 9: Final Prediction #
Monday, November 4, 2024
1 Day until Presidential Election
Election Day is tomorrow! I’m flying to Atlanta Tuesday morning and immediately heading to my polling station to cast my ballot after having a lot of trouble with the mail-in process. When I began this blog nine weeks ago, I had very little knowledge of the inner-workings of election forecasting and the kind of data that was fed into predictive electoral models. Over the course of the past two months, I have built models using simple linear regression, probabilistic models, and machine learning methods — all of which had varying levels of robustness and reliability. Some had predicted a Harris landslide, others heavily favored Trump. In the past few weeks, though, my selection of a singular model type and efforts toward regularization have converged the forecasts on an incredibly tight race between the two candidates. As any major forecaster will tell you, this election can go either way. The purpose of this blog post is to corroborate this idea and to make one final prediction before we begin to see results unfold tomorrow ( and likely over the course of this week).
Model Description & Coefficients #
## Warning: Option grouped=FALSE enforced in cv.glmnet, since < 3 observations per
## fold
For my final election prediction model, I decided to go with a LASSO regression. Throughout this semester, we have looked at a number of predictors that could have an impact on a presidential candidate’s vote share — from economic indicators to polling data to demographics to hurricanes and other shocks. With all these inputs in mind, I thought it most useful to find a method that selects only the most significant or useful features. This is the function of LASSO, which nullifies those predictors that are not as influential on the response variable. A lot of election forecasts run the risk of overfitting because they take in too much information and generate patterns of out of data that does not necessarily reflect reality. I thought it would be better to be conservative with selecting predictors and LASSO regression helped me do that.
Here, you can see the predictors and data that I decided to include in my LASSO regression model. I converged on these variables throughout the weeks by testing each of their relationships with a response variable of Democratic 2-party vote share. I included only those predictors which a significant impact on vote share: this includes a state’s voting behavior in past elections, state polling data, economic indicators, and campaign donation data. After having cross-validated to find the ideal lambda value for my LASSO regression, my model has nullified the Mean Democratic Poll Average variable. So, my final regularized model has corrected for a variable that I included, which might not actually have been that informative despite my previous regressions.


The first is the formula representation of my predictive model, where y refers to Democratic 2-Party Vote Share for a given state in a given election year. The second is a mathematical representation of the regularization objective that would occur for these predictors in particular.
To interpret the coefficients as they are represented above, we can say that, if a Democratic party were to receive 0% of the vote in the past two elections, the latest polling average for Democrats is 0, the Consumer Price Index is 0, there is no GDP growth for quarter 2 that year, and there are no campaign donations for the candidate, then the Democrat running that year in that state would get about 7.7% of the 2-Party vote share. Holding all other variables constant, as the Democratic vote share in the past election increases by a point so does the Democratic vote share in the upcoming election by .1257 points (and .0079 points with respect to a point increase in Democratic vote share in the second-to-last election). Holding all other variables constant, a point increase in the latest polling average for Democrats coincides with about a .98 point increase in Democratic 2-Party vote share in the upcoming election. Holding all other variables constant, a point increase in GDP Growth in Quarter 2 results in a .06 point increase in Democratic 2-Party vote share in the upcoming election. Finally, holding all other variables constant, a point increase in the log of campaign donations to Democrats results in about a .6 point decrease in the Democratic 2-party vote share in the upcoming election. All these coefficients seem intuitive except for the campaign donation variable. This representation is due to the logarithmic transformation of campaign donation data to scale its coefficient, but in reality, there exists a positive relationship between how much money a Democratic campaign rakes in and its eventual vote share. ( Refer to Week 6’s blog for more on this.)
## Loading required package: Matrix
##
## Attaching package: 'Matrix'
## The following objects are masked from 'package:tidyr':
##
## expand, pack, unpack
## Loaded glmnet 4.1-6
| Predictor | Lower | Upper |
|---|---|---|
| (Intercept) | -37.0735241 | 50.2256605 |
| D_pv2p_lag1 | 0.0000000 | 0.4574302 |
| D_pv2p_lag2 | -0.1224704 | 0.1576207 |
| latest_pollav_DEM | 0.4120334 | 1.5727115 |
| mean_pollav_DEM | -0.6909748 | 0.3996177 |
| CPI | -0.1254901 | 0.1407011 |
| GDP_growth_quarterly | -0.0994109 | 0.2102683 |
| log(contribution_receipt_amount) | -1.7544576 | 0.3380642 |
After bootstrapping the LASSO regression, we get the above range of coefficient values within a 95% confidence interval. It is peculiar that a lot of these predictors include 0 in their confidence intervals, which is troublesome for how much value we place on their significance. Nevertheless, their contributions to the model are still valuable to some extent. I will note, however, that the latest polling average for Democrat variable seems to be the most significant and that is reflected in its confidence interval (which does not include 0) and its large coefficient compared to other predictors.
Model Validation #
| Value | |
|---|---|
| R Squared | 0.8563942 |
| Mean Squared Error | 1.5842029 |
| Leave-One-Out Cross-Validation MSE | 2.7810769 |
To evaluate the robustness of my model, I rely on various model validation methods. First, I made sure to employ cross-validation within my LASSO regression, which minimizes the lambda squared error.
For in sample evaluation, I rely on R-Squared metrics and Mean Squared Error. For the coefficient of determination (R-Squared), I get about .86 which suggests a strong model. The Mean Squared Error is also relatively smalled compared to other models I have constructed in previous weeks. It is by no means small, though, especially considering that an MSE of this value in certain tight races could mean that a race swings either way.
For out of sample evaluation, I also rely on leave-one-out cross-validation. This gives me a higher value than the MSE, which is not the best but can be attributed to the small amount of observations that are used for this model. Realistically, there is not much data to work with for presidential elections, especially where economic indicators, demographics, and campaign donations are concerned. This is a constraint of all election forecasting models, and mine is not immune to it either.
Uncertainty #
| State | mean_dem | sd_dem | lower_dem | upper_dem | mean_rep | sd_rep | lower_rep | upper_rep |
|---|---|---|---|---|---|---|---|---|
| Arizona | 49.82247 | 1.249856 | 47.37275 | 52.27219 | 50.17753 | 1.249856 | 47.72781 | 52.62725 |
| Georgia | 49.83683 | 1.254854 | 47.37731 | 52.29634 | 50.16317 | 1.254854 | 47.70366 | 52.62269 |
| Michigan | 50.62857 | 1.298490 | 48.08353 | 53.17361 | 49.37143 | 1.298490 | 46.82639 | 51.91647 |
| Nevada | 50.93553 | 1.256353 | 48.47308 | 53.39799 | 49.06447 | 1.256353 | 46.60201 | 51.52692 |
| North Carolina | 49.77338 | 1.336243 | 47.15435 | 52.39242 | 50.22662 | 1.336243 | 47.60758 | 52.84565 |
| Pennsylvania | 50.11565 | 1.238461 | 47.68827 | 52.54303 | 49.88435 | 1.238461 | 47.45697 | 52.31173 |
| Wisconsin | 51.04669 | 1.292186 | 48.51400 | 53.57938 | 48.95331 | 1.292186 | 46.42062 | 51.48600 |
Just like I bootstrapped for my coefficients in the model, I am also bootstrapping for the Democratic 2-Party Vote Share for the battleground states to give more color to the uncertainty around my predictions. For every single swing state, the margin by which the predicted party “wins” is well within the standard deviation, or margin of error. This suggests that, while I am converging on one party to win for a given swing state, they are all toss-ups and either party can realistically win them. That is, my model is not determinative. Still, I place some trust in the mean_dem and mean_rep vote share predictions for the swing states above for the sake of this endeavor and my work of the past few weeks. The states colored in blue are those where the point prediction for Democrats (with 2-Party vote share) is higher than it is for Republicans. The states colored in red are those where the point prediction for Republicans (with 2-Party vote share) is higher than it is for Democrats. The standard deviations for all swing states is relatively the same.
Electoral College Visualization #
| State | Predicted Electoral Votes | Winner |
|---|---|---|
| Alabama | 9 | Republican |
| Alaska | 3 | Republican |
| Arizona | 11 | Republican |
| Arkansas | 6 | Republican |
| California | 54 | Democrat |
| Colorado | 10 | Democrat |
| Connecticut | 7 | Democrat |
| Delaware | 3 | Democrat |
| District Of Columbia | 3 | Democrat |
| Florida | 30 | Republican |
| Georgia | 16 | Republican |
| Hawaii | 4 | Democrat |
| Idaho | 4 | Republican |
| Illinois | 19 | Democrat |
| Indiana | 11 | Republican |
| Iowa | 6 | Republican |
| Kansas | 6 | Republican |
| Kentucky | 8 | Republican |
| Louisiana | 8 | Republican |
| Maine | 4 | Democrat |
| Maryland | 10 | Democrat |
| Massachusetts | 11 | Democrat |
| Michigan | 15 | Democrat |
| Minnesota | 10 | Democrat |
| Mississippi | 6 | Republican |
| Missouri | 10 | Republican |
| Montana | 4 | Republican |
| Nebraska | 5 | Republican |
| Nevada | 6 | Democrat |
| New Hampshire | 4 | Democrat |
| New Jersey | 14 | Democrat |
| New Mexico | 5 | Democrat |
| New York | 28 | Democrat |
| North Carolina | 16 | Republican |
| North Dakota | 3 | Republican |
| Ohio | 17 | Republican |
| Oklahoma | 7 | Republican |
| Oregon | 8 | Democrat |
| Pennsylvania | 19 | Democrat |
| Rhode Island | 4 | Democrat |
| South Carolina | 9 | Republican |
| South Dakota | 3 | Republican |
| Tennessee | 11 | Republican |
| Texas | 40 | Republican |
| Utah | 6 | Republican |
| Vermont | 3 | Democrat |
| Virginia | 13 | Democrat |
| Washington | 12 | Democrat |
| West Virginia | 4 | Republican |
| Wisconsin | 10 | Democrat |
| Wyoming | 3 | Republican |
| Winner | Electoral Votes |
|---|---|
| Democrat | 276 |
| Republican | 262 |
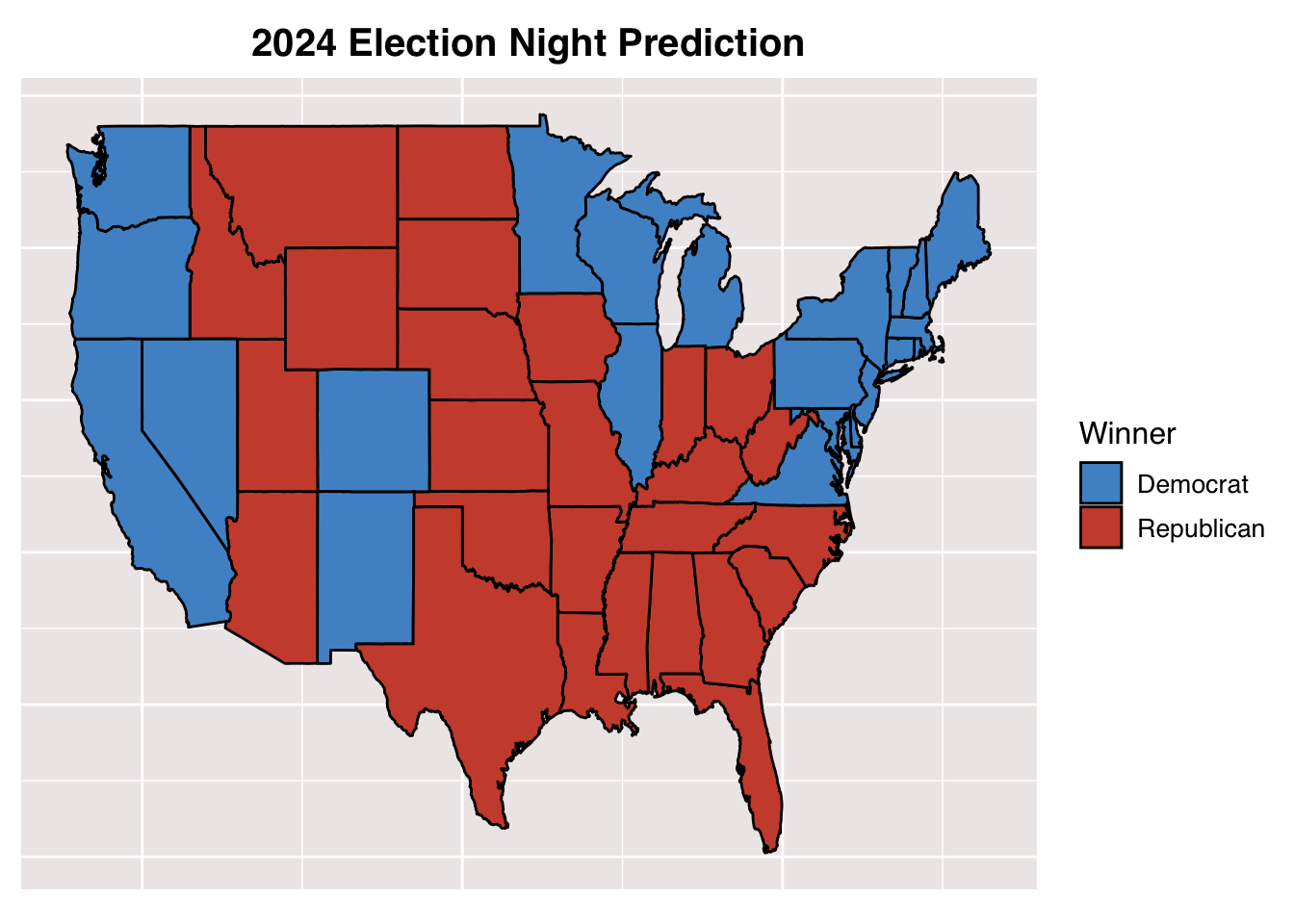
Putting my bootstrapped point predictions into play, I have constructed a final electoral college prediction above. Of the swing states, the Republicans are expected to take Georgia (my home state), North Carolina, and Arizona. The Democrats are expected to take Pennsylvania, Wisconsin, Nevada, and Michigan. This puts the Democrats just barely over the 270 needed to win the office. If this prediction were true, it would make the 2024 election one of the closest in recent history, second only to the 2000 election between Bush and Gore.
Conclusion #
According to this week’s model, Harris will win the 2024 Presidential Election, taking 276 electoral votes.
My models for the past few weeks have been wavering between a Harris victory and a Trump victory by incredibly close margins. This is an incredibly close race, and we should not be surprised by the results. Thank you for following along for the past couple of weeks. Thank you to the GOV 1347 teaching staff for their help throughout the semester with content questions and technical difficulties. Thank you in particular to Matthew Dardet for all his guidance and Prof. Ryan Enos for his incredibly insightful lectures. Hopefully soon, we will see how my prediction fares. Until then, take care!
Sources #
“US Election Results: When Will We Know?” Global News, 4 Nov. 2024, https://globalnews.ca/news/10834744/us-election-results-when-will-we-know/.
Polling Data Provided by GOV 1347: Election Analytics teaching staff (which drew from the FiveThirtyEight GitHub)
Economic Data Provided by GOV 1347: Election Analytics teaching staff (which drew from the Bureau of Economic Analysis and Federal Reserve Economic Data)